Scales and Tuning

The impact of a musical composition is created by the relationships that exist between successive notes, rather than the actual pitch of each note. These relationships are essentially mathematical in nature and are as important to music as proportion is to architecture.

• The perception of pitch is often subjective, being influenced by harmonics, also known as upper partials, or other noises produced by the instrument in question.
• Unlike pitch, the frequency (f) of a musical note is a scientifically-measured rate at which a cyclic oscillation reaches the same point in its period. This is given in cycles per second (c/s) or hertz (Hz), but doesn’t always relate exactly to the subjective pitch of a sound.
• Each doubling of a frequency is known as an octave. As the frequency of a sound increases in a geometric progression (2f, 4f, 8f …) so the pitch is perceived as increasing in an arithmetic manner (1 octave, 2 octaves, 3 octaves …).

Most music is based on scales, sequences of notes that produce a pleasing or emotional effect. The Western world normally uses equal-tempered tuning, in which each octave is divided into twelve semitones, and all other intervals are considered as multiples of these semitones.

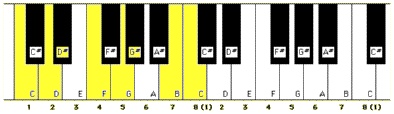
• Pairs of notes with a given interval always have frequencies that are in the same ratio. For example, all notes an octave apart have a frequency ratio of 2:1 and all notes a Perfect 5^th apart (7 semitones) are in the ratio 3:2.

Modern Keyboards

The standard musical keyboard, with its eight white notes of C, D, E, F, G, A, B, C and five raised black notes in each octave, was developed from the scales employed in Western music. Its ability to perform polyphonic compositions has had a huge influence on musical progress.

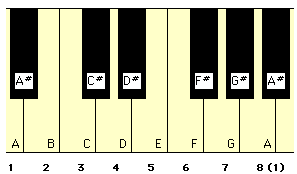
The following diagram shows the layout of a modern keyboard and its ‘important’ notes. It indicates both the scientific notation for notes, as commonly used by musicians who work with MIDI, and Helmholtz notation, as favoured by academics. It also shows traditional note names.

As you can see, such a keyboard spans just over seven octaves. On most keyboards each octave is around 6½ inches wide, which is usually within the scope of the human hand.

• The ‘octave up’ mark, as in A', meaning an octave above the current note of A, is sometimes used independently of standard Helmholtz notation.
• The note of A4, above middle C, is usually tuned to 440 Hz, also known as Standard A.

An Introduction to Scales

An octave is far too large to be used as a unit of pitch and must therefore be divided up into intervals that are repeatable and musically pleasing. A scale consists of intervals starting from a given note and rising up in degrees through an entire octave.

• The starting note for a scale is called the key signature, key or tonic. The tedious process of converting music or musical script from one key to another is called transposition.

Pythagoras and his Greek contemporaries in the 4^th century BC divided the octave into seven intervals to form a scale with the notes represented by the first fifteen letters of the Greek alphabet. Today, the eight notes marking the boundaries of these intervals have the letters A, B, C, D, E, F and G, matching the white notes on a modern keyboard, as shown below.

The basic interval, the spacing between the notes, is known as a whole tone or tone. Today, any scale that only uses these larger intervals is referred to as a whole tone scale. Normally, such a scale has only two possible starting points, C or C sharp (C#). Unfortunately, this kind of a scale, in which all the steps are equal, isn’t particularly pleasing to the ear. Therefore, in a modern scale some of the seven intervals are usually reduced to half a tone, also known as a semitone.

• If the note of A is raised by a semitone it becomes A sharp (A#). Similarly, if lowered by a semitone it becomes A flat (Ab). Notes that are neither sharp nor flat are called natural.

Modes

The earliest of the musical modes used by the Greeks are believed to be based on the notes of D, E, F and G. All of these modes consist of scales that travel over a single octave, using only the ‘white’ keys of a keyboard, plus two semitone intervals that were introduced to add extra character to the music.

The later modes employed in medieval music give the same results whatever note is used for the start of the scale. This allows instruments that are tuned differently to be played together. Since there is no absolute tuning reference each instrument can be tuned by means of the beat-less fifths method (see below), a technique that allows a musician to compare the pitch of one note with another.

The Ionian mode, in its 16^th century form, uses the white notes of the keyboard from C to C and is equivalent to the modern scale of C major, as shown below. This has semitone intervals between the 3^rd and 4^th white notes and also between the 7^th and 8^th notes.

Also favoured in the 16^th century, the Aeolian mode employs the white keys from A to A, and is equivalent to the modern scale of A minor, shown below. It has semitone intervals between the 2^nd and 3^rd notes and between the 6^th and 7^th notes. The melodic minor scale variation has both the 6^th and 7^th notes sharpened, whilst in the harmonic minor scale only the 7^th note is sharpened.

Other Greek modes based on the white notes included Dorian (D to D), Phrygian (E to E), Lydian (F to F) and Mixolydian (G to G). These scales, which were revised in the 4^th century by Saint Ambrose, in the 6^th century by Saint Gregory, and by Henry of Glarus in the 16^th century, are sometimes still used to evoke a ‘high church’ feel to music.

By the end of the 17^th century the earlier modes had all been replaced by modern scales.

Other Scales

The following are sometimes used as an alternative to standard modern scales:-

Intervals

Modern scales are diatonic, meaning that both tone and semitone intervals are used. All such scales rise by seven notes in each octave, the eighth note being one octave above the first. There are typically five tones and two semitones in an octave, organised to suit a major scale or minor scale.

Musical terminology employs intervals to define the distance between any pair of notes. An interval usually has a specific name as well as a generic name, as in a Minor 3rd interval, where Minor is the specific name and 3rd is generic. The latter name is simply an inclusive count of all the notes that exist between the notes. So, looking at our standard keyboard, as shown below, we can see that interval from C to E is a 3^rd, since it spans three notes. Similarly, A to C and B to D are also a 3^rd.

Specific names are set by the key signature of the lower note (key signatures are dealt with elsewhere in these guides). For example, the generic name of the interval from C to Eb is a 3^rd. However, the specific name depends on whether the upper note is in the key signature of the lower note. If so, it’s a major interval or perfect interval, with the Major name used for 2^nd, 3^rd, 6^th or 7^th intervals and Perfect for 1^st (prime), 4^th, 5^th or 8^th (octave) intervals. An interval ending a semitone lower than a major or perfect interval is called a minor interval, whilst one ending a further semitone down is known as diminished. Finally, an interval ending a semitone higher than a major or perfect interval is said to be augmented.

Much of this is summarised by the following table, which also indicates frequency ratios, examples from the note of C and a count of inclusive semitones:-

Each perfect interval, such as a Semitone, Tone, Perfect 4^th and Perfect 5^th, ‘fits’ exactly within the octave. In a major scale, where the starting note is on a white key, these also fall on white notes. In addition, such intervals have frequency ratios containing consecutive numbers, relating to the mathematical perfection defined by the Golden Mean.

The major intervals shown here are larger than the equivalents in a minor scale. For example, a Major 3^rd covers five semitones in all, whilst a minor scale has a minor interval of a Minor 3^rd, which is only four semitones. Like perfect intervals, all the major intervals in a major scale land on on white notes. However, the use of even-tempered tuning (see below), causes the frequency ratios to become increasingly peculiar towards the top end of the octave.

The remaining intervals are augmented and diminished, indicating that a semitone has been either added to or removed from a perfect or major interval. This gives a sharpened or flattened result that lands on the black notes in a major scale. Fortunately, even-tempered tuning and enharmony (see below) ensure that a note such as Db actually produces the same pitch as C#, although this isn’t the case for other tuning methods.

The diagram below shows the intervals for white notes in the scale of C major:-

Intervals greater than an octave can be given as a compound interval, consisting of one or more octaves and a smaller interval. Thus the interval from C to G' (the latter being in the next octave) can be given as a compound interval made up of an octave (C to C') and a Perfect 5^th (C' to G').

• An interval can be played harmonically, in which all the notes have to be sounded simultaneously, or melodically, with one note played after the other.

Recognising Intervals

Intervals aren’t always easy to recognise, although the following table can help:-

Scales in Detail

All scales contain eight degrees, which are measured as standard intervals. These degrees begin at a given note or tonic, which also gives its name to the scale. The degrees are as follows:-

Major Scales

In all major scales the 3^rd degree is two tones above the tonic, as shown below:-

Looking at this carefully, you’ll see that the notes of a major scale are actually spaced as follows:-

The simplest major scale is that of C major, which consists of the notes:-

which appears on the keyboard as:-

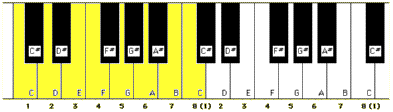
Now, if you tried to play a scale in E major, you might expect to play:-

but you would be horrified at the results. Instead, you must play those notes that are spaced according to the tone-semitone pattern described above, which are:-

and look like this on the keyboard:-

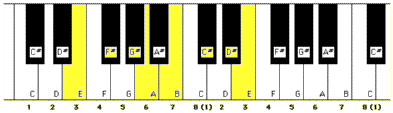
These and all other major scales are alike, in that the intervals between successive notes are the same, irrespective of the starting note. And, unlike some types of minor scales (see below), the same notes are played whether you are ascending or descending the scale.

Minor Scales

In a minor scale the 3^rd degree is only one tone and a semitone above the tonic, as shown below:-

Minor scales are divided into the types described below. Note that all the scales belonging a particular type have the same intervals between the notes.

Natural Minor Scale

This follows the degrees described in the above section. For example, the natural scale of C minor is:-

which, according to the rules of enharmony (see below) can be written as:-

and looks like this:-

Melodic Minor Scale

Unlike other scales, this scale uses different notes, according to whether you’re moving up or down the scale. For example, when ascending, the following notes are used in the melodic scale of C minor:-

which looks like this:-

but when descending it goes down the keyboard using the notes:-

which, with the application of enharmony, looks like:-

Harmonic Minor Scale

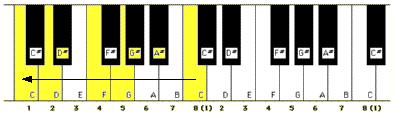
The harmonic scale of C minor consists of the following sequence:-

which looks like this on the keyboard:-

Enharmony

As already mentioned, a flattened note in an even-tempered scale is equal to the sharpened version of the next tone down. This is known as enharmony. For example, the scale of F major is:-

but this would be confusing whilst reading music in this scale, since the sequence contains two A notes. Instead, this scale is normally written as:-

Enharmony also refers to other equalities in intervals. For example, an Augmented 3^rd from C is E#, whilst a Perfect 4^th from C is F. In practice, both intervals in an even-tempered scale result in the note of F.

• Where even-tempered tuning isn’t used, enharmony is a measure of the difference in pitch, usually very small, between tones produced by flattening or sharpening of adjacent notes.

Tonic Sol-fa

This form of scale notation, introduced by J S Curwen in the 1840s as an aid to sight reading, is named after sol fa, the C located one octave above middle C. The system uses the words doh, ray, me, fah, soh, la and te for the notes, as derived from do, re, mi, fa, sol, la and si in Italian. The diagram below shows the tonic sol-fa scale, as normally used in the key of C major:-

As you can see, tonic sol-fa doesn’t assume that all sharps (fe, se, le…) in an ascending scale will give the same pitch as the flats (ta, la, ma …) produced in a descending scale. Although they can be the same, they frequently sound different when you use an actual instrument to play real scales.

• Changing the key can shift the starting point of the scale, so that doh can be a flat or sharp note.

Chords

A chord consists of two or more intervals played together, often resulting in very complex and changing harmonics. Like intervals, chords can be played harmonically, involving playing them all at once, or melodically, in which they’re played one after the other. An arpeggio chord or glissando is slightly different, in that all the notes are played quickly in succession, whilst in a portamento the pitch is slurred across the notes. However, both of the latter playing techniques can create rich musical textures similar to chords.

The following types of chords are commonly encountered:-

• The fundamental note of a chord, also known as the root or keynote, gives its name to the chord.
• A major chord usually adds a comfortable element to a tune, whilst a minor chord can seem frightening or unpleasant. Both augmented and diminished chords can add tension to music, producing within it a need for resolution, either upwards for a diminished chord or downwards for an augmented chord.

Three-Note Chords

Most chords consist of at least three notes:-

One of the simplest three-note chords is C major, which is written as C and made up of the following:-

whilst the E minor diminished 5th chord, written as Emb5, consists of the following notes:-

Five-Note Chords

Some chords contain up to five notes, as shown here:-

The five-note chord of D minor flat 5th, major 7th, diminished 9th, written as Dmb5/7Mb9, consists of the following notes:-

Chord Inversion

A normal chord usually contains a 3^rd, 5^th, 7^th and 9^th degrees based on the fundamental. Inverting a chord changes this order. A first inversion shifts the fundamental up to the next octave, making the 3^rd the bass note, whilst a second inversion also pushes up the 3^rd, making the 5^th the lowest note. This process can continue, as shown here for the C Major 7th chord:-

• Chord inversions don’t change the pitches in a chord, only the octaves.

An alternative process, known as bottom inversion, can also be used, where bass notes are pushed into the previous octave. The following table summarises the order of notes when using all the various forms of inversions:-

where F is the fundamental and the numbers are the degrees.

The Three Chord Trick and Cadences

The three chord trick is a special sequence of chords, commonly used to great effect in jazz and blues (generally in a 12-bar format for the latter), although they can also be found used in other styles of music. The usual sequences are:-

and so on. All of these involve a shift upwards of five semitones followed by two semitones.

Other cadences or progressions of chords can also be useful. A perfect cadence, for example, progresses from the dominant chord to the tonic chord whilst a plagal cadence moves from the subdominant to the tonic. An imperfect cadence, on the other hand, progresses from the tonic, or another chord, to the dominant, whilst an interrupted cadence moves from the dominant to submediant, or another chord that replaces the expected tonic chord.

Tuning Techniques

A modern musical synthesiser derives its tuning from an accurate crystal reference which means it doesn’t usually need tuning. Sadly, conventional instruments aren’t that easy.

In a sinusoidal waveforms the measured frequency and subjective pitch coincide, allowing a simple electronic tuning meter can be used. Unfortunately other waveforms contain components that create an apparent discrepancy between frequency and pitch. Any instrument that produces such components must be tuned by using the traditional musical tuning techniques described below.

The Tuning Reference

The tuning of an instrument is usually based on the frequency of a particular note, other notes then being tuned in relation to this reference. The international standard of 1939 sets middle A (the A above middle C) to 440 Hz, this being known as Standard A. Tuning an instrument to this convention puts middle C at 261.6 Hz, and the higher C at 523.2 Hz.

Recent wind instruments are sometimes said to have low pitch, since they’re designed to operate with this modern form of tuning. However, older instruments are intended for high pitch, which is almost a semitone higher and still used by some brass bands. Older high pitch standards of tuning, such Old Philharmonic pitch and New Philharmonic pitch, are now obsolete, although some countries continue to use higher pitches, with A set to 442 Hz or even 444 Hz.

Tuning the Other Notes

The table shown below gives the theoretical frequencies for musical notes, based on middle A being at 440 Hz. As mentioned above, using frequency values can give odd results with real sounds.

The two commonest methods of tuning these notes are described below.

Natural Interval Tuning

As mentioned above, many traditional instruments are tuned for natural intervals by means of a beat-less fifth. Since a Perfect 5^th has a ratio of 2:3, the principle can be easily demonstrated using frequencies such as 200 and 300 Hz . If the 300 Hz fundamental goes ‘out of tune’ to 300.5 Hz its second harmonic will be 601 Hz. This will beat with the 3rd harmonic of 200 Hz to give an audible frequency of 1 Hz, corresponding to exactly ten ‘beats’ in every ten seconds.

This tuning procedure begins by setting middle A (the A above middle C) to the frequency used for standard A, usually 440 Hz. You then start tuning using pairs of notes as follows:-

as in the following sequence:-

At the end of this process A (the note you started with) will come out at around 434 Hz! This considerable difference is known as the comma of Pythagoras. Natural intervals are more widely spaced (sharper) than tempered intervals, meaning that an instrument tuned in one key can be as much as a semitone out of tune when used in a different key.

Tempered Interval Tuning

Modern keyboard music is based on the even-tempered scale, a system particularly favoured by the pioneering composer Bach. It’s main advantage is that it gives consistent results, whatever key is chosen. This is because the frequencies of all 12 intervals are all in the ratio of 1:12 √2.

In tempered tuning, only A and its octaves are tuned exactly. The error caused by the comma of Pythagoras is then absorbed by spreading it evenly across each octave. This means that all the semitone intervals within the octave are actually tuned to be slightly flat.

Tempered tuning uses the beats method, a variation of the beat-less fifths system described above. As before, the procedure begins by tuning middle A to standard A at 440 Hz. Then A' (the A in the next octave) is tuned to 880 Hz in relation to A. Then D, which is a 5^th below A, is tuned by first setting it flat and then advancing the tuning past the beat-less point until the required beat is obtained.

Further adjustments should then be made to give the following results:-

• An error of 4 to 5 beats on the final E to A interval is considered perfectly normal.
• Five beats of inaccuracy in 10 seconds means an error of 0.5 Hz in the second harmonic, or just 0.25 Hz in the fundamental, which is actually very accurate.
• The differences between natural and tempered scales can be particularly noticeable when stringed instruments are used to accompany a piano.

The following diagram shows the sequence of tuning when applied to a keyboard.

References

American Concise Encyclopedia, Zane Publishing Inc, 1996

Dolmetsch website at www.dolmetsch.com

Music Theory Reminder Lexicon, author unknown, 1999

©Ray White 2004.