
All buildings, whatever their style, are made from geometrical forms, which are then overlaid with further detail or decoration. The basic elements are:-
Most buildings have rectangular elements, both in elevation and plan. Walls constructed this way can be used to create strong ‘box’ structures, with square rooms that are convenient for internal furniture and fittings. Rectangles also define the height and width of a building, giving it a perspective within the landscape, relating it to the horizon.
Traditional roofs and gables are triangular, often with a central roof ridge along the length of a building. This ‘pitched roof’ style is frowned on by many in the modernist movement, driving many architects to use a flat roof, which invariably leaks, or an ‘angled slab’ form of construction, which makes the building look like a shed or ‘lean-to’.
Apart from rotundas, windmills and towers, few buildings use circles as a primary element in their plan, and even fewer use it in the elevation. Although a circular plan is attractive in theory, the difficulties associated with curved walls make it impractical. However, the circle can be used in other complex ways, as in arches, roof vaults, bow window bays and ‘wagon’ windows. These features can imbue a building with a tremendous charm and a quality of timelessness.
Multi-sided buildings suffer from the similar problems to those having a circular plan. Other polygonal elements can be rare, although they often appear in partial form, as in unusual styles of arches or in the plan of an angled bay window. In common with pyramids, the polygon gives a building an air of mysterious antiquity.
A skillful architect can assemble all the necessary elements to create a building that is not only pleasant and comfortable, but also visually stimulating. However, this is only possible when all the parts fit together properly and in proportion. In the author’s opinion this requires a deep understanding of where human beings fit into the universe.
At first glance it might appear that the matter of proportion is really a matter of taste. In fact, everything in nature follows certain rules, which, if applied to buildings or other objects, gives them a pleasing appearance.
To understand the principles of proportion we must investigate some rather strange geometrical and mathematical concepts. Consider the following line, which has been divided into two parts:-

Now the relative proportions of A, B and C can be evaluated as follows:-
B = 8 = 1.600 A = 13 = 1.625
C 5 B 8
Notice how these particular dimensions result in a similar result for both calculations: this is known as the Golden Section. This effect is apparent when using adjacent pair of numbers in the Fibonacci series, as shown here:-
where each number in the series equals the sum of the two previous numbers. The ratios of two successive numbers in this sequence have the peculiar characteristic already mentioned, as shown in the following examples:-
8 = 1.600 13 = 1.625
5 8
21 = 1.615
13
You can carry on working out these values if you like, although you’ll find that the ratios of successive terms always tends towards a value of 1.6180339887499, which is known as the Golden Mean. This value, which is one of those ‘magic numbers’ that occur in the universe, is given the name Φ (phi).
This constant is just as important as the value of π (pi) in geometry, which is 3.141592653589793, or the value of e (exponent) in maths, which is 2.718281828459045. In fact, Φ is related to π by the following equation:-
In addition, Φ is also the only value that satisfies this equation:-
This is a strange characteristic, since the left hand side of the equation is a typical element in arithmetic or linear progressions whilst the right hand side appears in square-law progressions. In fact, this explains the importance of Φ in music, where perceived pitch rises one octave for every doubling of frequency. Common musical relationships include major 3rd (4:5), perfect 4th (3:4), perfect 5th (2:3) and major 6th (3:5), as well as the octave (1:2) itself.

This diagram illustrates how the value of Φ can be determined by using geometry instead of mathematics.
The triangle in the gable of a building often consists of two ‘reflected’ shapes of this form.
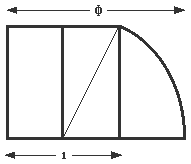
The next illustration shows another way of obtaining Φ geometrically, this time by dividing a unit square into two, drawing a line across the diagonal of the right-hand rectangle so produced and then using the latter to create an arc down to the base line. Another example, this time with circles, is shown below. 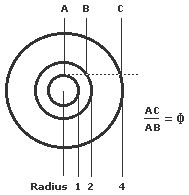
The influence of Φ is apparent in the constituent parts of many buildings, especially those of classical origin.

Shown here is the Golden Rectangle, which can be produced using ratios of 3:2, 5:3, 8:5, 13:8, 21:13, 34:21, Φ:1 or 1:1 ⁄Φ. This element is often used in classical architecture, as shown below.

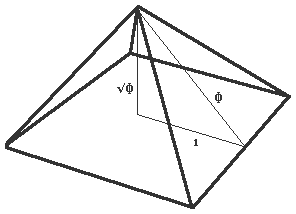
The Egyptians were also aware of the values of Φ and π, leading them to create pyramids. all of which have identical proportions. Each has a height equal to the radius of a circle whose circumference equals the perimeter of its square base. This gives an angle of 51° 51′.
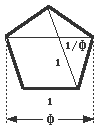
The pentagon, which appears in some buildings, is also related to Φ, as illustrated below.
The materials used in the finishing of a building have a significant effect on the visual impact of a structure. Traditionally, external surfaces are of stone (either quarried or reconstituted), baked clay (in the shape of bricks or tiles, with or without glazing), plaster (known as pargetting when used decoratively), cement (also known as stucco) or wood (either forming the building’s framework or as a shiplap covering), with windows occupying only a small part of the elevation.
The limitations of early forms of transport ensured that the materials used in older buildings, were supplied from the local area. Even so, more prestigious buildings were often constructed using materials moved over wider distances.
Modernist architects sometimes use cement disguised with white paint, but generally favour exposed concrete, steel and glass. Unfortunately, these often clash with the traditional materials of older buildings in the vicinity and lack any regional identity. Furthermore, the use of earlier materials in modernist buildings creates something that’s ‘neither fish nor fowl’.
Concrete, once thought to be the answer to all our problems, has been a huge disappointment. Even when initially finished to a high standard it ‘weathers’ badly, resulting in grubby-looking buildings and structures. Worst of all, modern ‘flat-faced’ designs don’t allow for the flow of rainwater, resulting in a facade covered in those familiar and unpleasant black streaks.